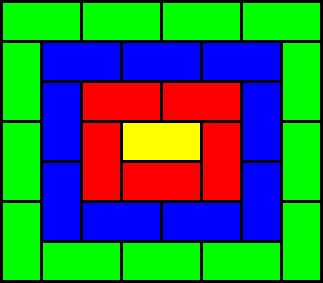
Considerate un rettangolo 1×2, come quello giallo al centro della figura qui a fianco. È possibile circondarlo completamente, senza lasciare spazi vuoti, con cinque rettangoli uguali, quelli rossi. La figura ottenuta può a sua volta essere circondata da nove rettangoli (blu), e ancora da tredici rettangoli (verdi), e così via all’infinito. Ma se avessimo avuto un cerchio al posto del rettangolo non saremmo mai riusciti a completare nemmeno una corona. E il problema non è tanto dovuto al fatto che il cerchio sia una figura curva: se per esempio togliamo due quadratini piccoli da un lato lungo del rettangolo di partenza, il problema è comunque impossibile.
Bene: come spiega Wikipedia, queste due figure hanno numero di Heesch rispettivamente infinito e zero. Più precisamente, il numero di Heesch di una forma bidimensionale è il massimo numero di anelli circolari (o corone), costituite dalla stessa forma, che si possono costruire attorno ad essa, senza sovrapposizioni e senza spazi vuoti. Il problema di Heesch consiste nel chiedersi se esistono forme geometriche ch hanno un numero di Heesch qualunque tra 0 e infinito. Heinrich Heesch ideò il problema quando nel 1968 scoprì una forma (mostrata in nero nella figura di destra) che all’inizio pare poter tassellare il piano come i quadrati, ma che si blocca subito: il numero di Heesch corrispondente è 1. Si è poi scoperto che nel 1928 Walther Lietzmann aveva già trovato una figura con numero di Heesch 1, che assomiglia ai puntatori di Google Maps :-)Nella voce di Wikipedia potete trovare esempi di figure con numero di Heesch da 1 a 6, il massimo che si è scoperto finora. Qui mostro solo il più piccolo polimino con numero di Heesch 2, che può far capire come il problema non sia affatto facile da risolvere: chi si immaginava che una figura così arrivasse ad avere due corone?
What time is Jujutsu Kaisen Season 3 Episode 3 out?